wheatgreaser

square root of geometry, my ass

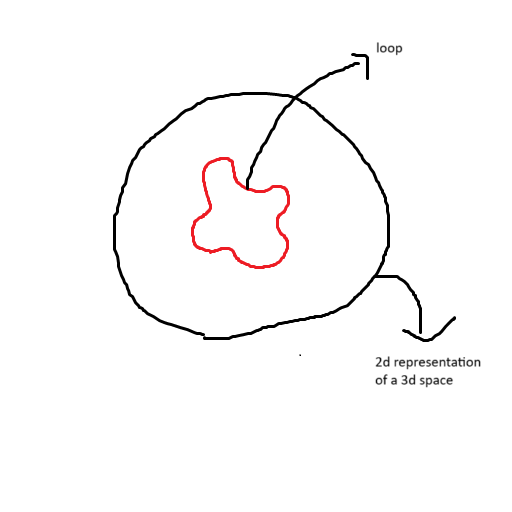
first we need to steal some terms from topology.

homotopic: two loops can be called homotopic if they can be changed into one another without cutting and gluing. simply connected: a space is simply connect if a loop can shrink down to a point. lets say there is a hole. if the hole is inside the loop then it cant shrink down to a point, so its said to be of a different homotopy class (homotopy class: a loop belonging to a particular homotopy class can transform into al the loops in the same class, i.e, they are all homotopic) winding number: number of times a loop winds/loops around the hole, it can belong to the set {0, 1, 2, …}. note that this only for the specific example of a hole in a whiteboard. a loops having a certain winding number cannot be transformed into a loop having another winding number. these loops are super useful because they tell us something about the space they live in.

we also need to fuck around with rotations, they’re crucial too, so the normal way of rotating is by specifying an axis and an angle, we can just rotate an object around the axis by a certain angle. so we can represent this by using an axis angle vector, the direction of which specifies the axis and the magnitude of which represents the amount of rotation. now we’ll notice something interesting, when we rotate a cube by 180 degrees the rotation, the magnitude continuously increases till 180 and then the vector flips and the magnitude starts decreasing.

now we need to think about this vector topologically, so lets imagine all the possible rotation vectors, so its obviously a sphere with radius 180 degrees (or pi radians) now when the radius vector continuously increases and touches the boundary of the sphere, it gets teleported to the opposite side.

now lets brindg in our loop fuckers to understand more about the space we’ve conjured up. so we can represent a wiggle like this:

now this loop represents a wiggle (because we didnt touch the circuluar boundary (only then we complete a 180 degree turn))

now there can be another class of loops like this:

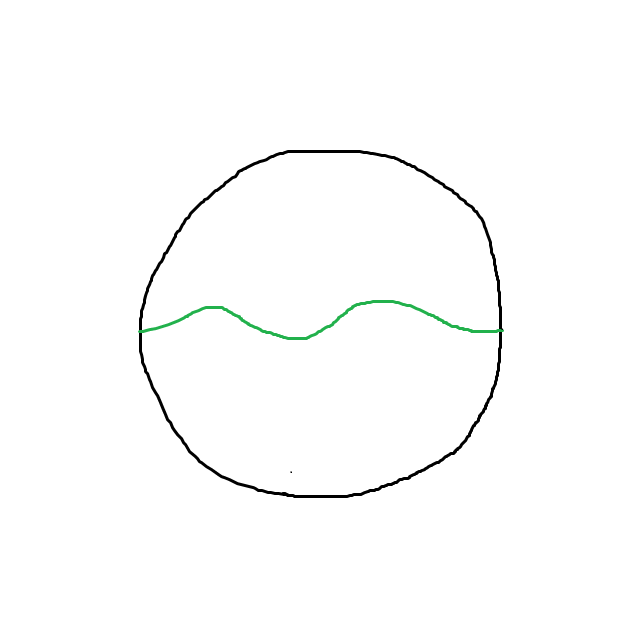
this undergoes a complete rotation also note that the two boundary points connected by the green “loop” is the same point. this is a whole nother class of loop because it cannot be squished into a point, i.e, its not simply connected. there are only two type of homotopy classes in this type of space, one if there are odd number of border crossings and another if there are even number of em. we call a loop class 1 if it has odd number of border crossings and class 2 if it has even number of them. NOW WE CAN GET ALL DIRTY AND ALGEBRAICCCC.

fuck I forgot about this post halfway.