wheatgreaser

can you markov my chain?

july 17, 2024:

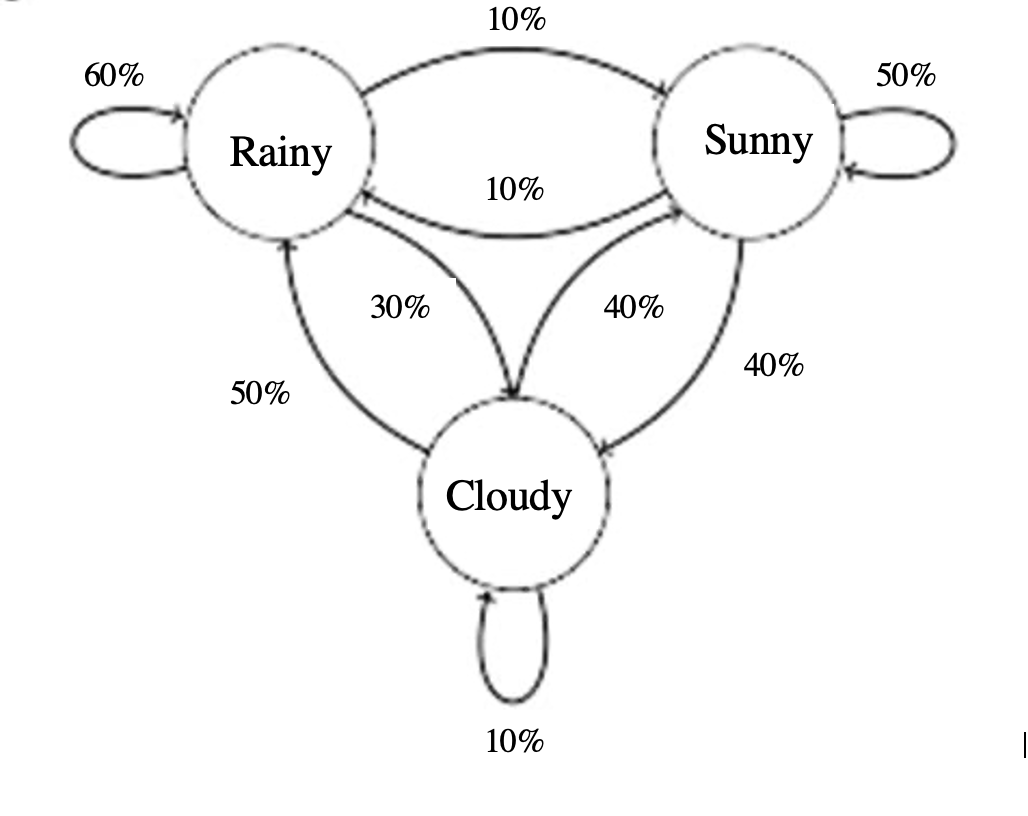
markov chains are simple. the future state only depends on the current state. its as simple as that. look at this image (its an order):

source: towardsdatascience

ok lets look at the node labelled as rainy, the arrows basically just give the probability of the future state given the current state(rainy). so, for example the probabiltiy of it raining tomorrow (future state) given that its raining today (current state) is is 60% (indicated by the arrow pointing to itself). its that simple. and obviously the sum of the outgoing arrows should be 100% or if you’re talking about fractions it should be 1.

ok so in essence, i want to program something that will find the probability of a random state, for example what is the probabiltiy that it will rain on a random day given a “directed graph” (the image).

july 18, 2024:

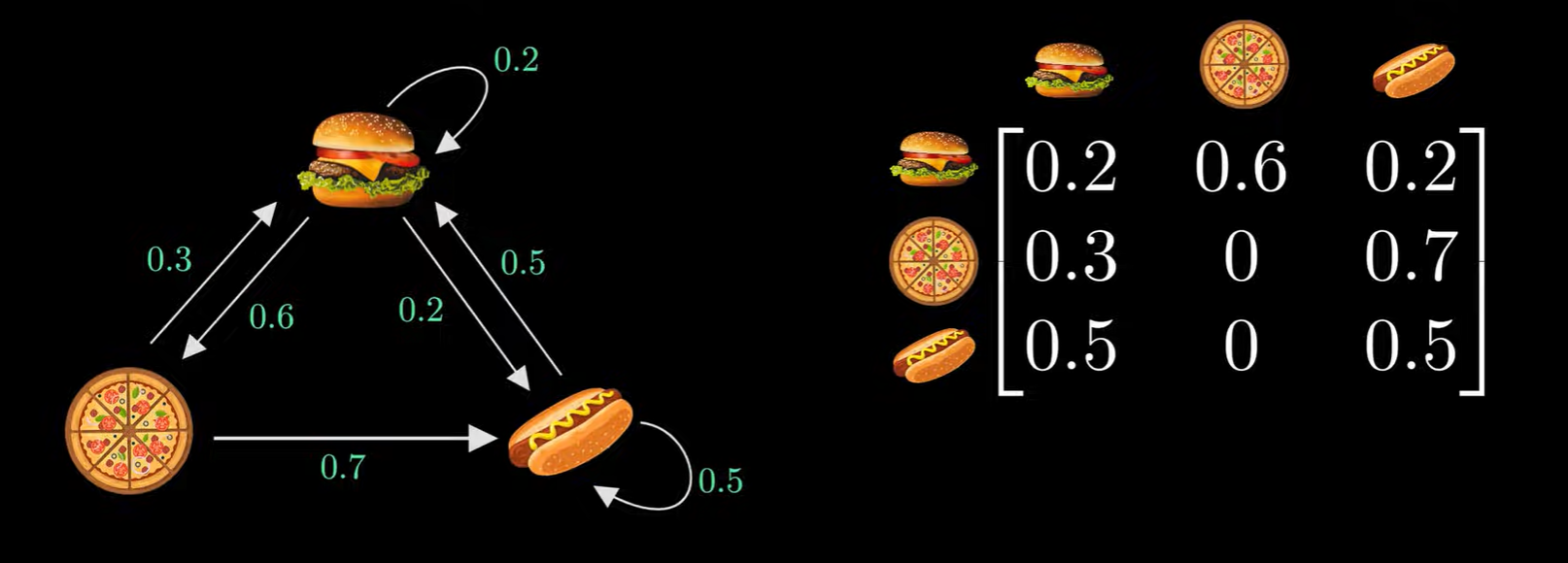
now the way I thought involved going through like a huge number of states (a random “walk” if you will) and then computing the individual probabilities. but its apparently a stupid solution and i should be put in a loony bin for even thinking of it. the “elegant” way to do it involves linear algebra. eigenvalues. yes. now the intial way that i conjured about involved making a “node” class and creating the directed graphs using that, but there’s a better way to do that. we can represent it as an adjacency matrix.

source: https://www.youtube.com/watch?v=i3AkTO9HLXo

we basically map from row TO the column for example, the relationship between the burger TO the hot dog is encoded as thefirst row (burger row) and 3rd column(hot dog column). next we have another 1 x 3 matrix that shows the probability distribution. so for instance if it is a pizza day it will be shown as [0, 1, 0]. if we multiplay this with the adjacency/transition matrix we’ll get the probability distibution indicating the future states.

source: https://www.youtube.com/watch?v=i3AkTO9HLXo

so if we pass in this result again we get a new probability distribution which indicates the proabbailites of the 3rd state given that the first state was pizza. if we get the same distribution twice, let’s say on the 10th iteration of this process that means that we have got ourselves the probability distribution of a state on any step of the walk independant of what we started with. so mathematically its something like A * p = p here we need to find p and can y’all remind me what we call a vector that is invariant under a linear transformation (multiplying with a matrix), yup. eignvectors. told you. so this has become an eigenvector problem.

ok, we’re gonna be using the jacobi method to find the eigenvector, its basically an iterative method to find the zeroes (‘cause we do (A - I) * p = 0 to find p). i dont exactly know how it works, okay? shut the fuck up. maybe i’lll dive into it in a future log. anywho, we can find the eigenvector using that method and we obviously set the eigenvalue to 1 badabingbadaboom we have the probability distribution.